Welcome to London Grip, a forum for reviews of books, shows & events – plus quarterly postings of new poetry. Our most recent posts are listed below. Older posts can be explored via the search box and topic list. For more information & guidelines on submitting reviews or poems please visit our Home page.
I suspect few London Grip readers will have heard of Charles Broyden (1933-2011) even though he is the originator of one of the twentieth century’s most significant ideas in computational mathematics. Non-mathematical readers may be relieved to learn that I won’t be trying to explain what this idea was (although a few key expressions appear in the image on the right)! This article – which I hope will be of interest to non mathematicians – has its origins in a quotation from Broyden’s obituary [1] which states – using the subject’s own words – that he left university in 1955 armed with an indifferent bachelor’s degree in physics and an uncertain hold on linear algebra. These qualifications were enough to secure him a job in industry and the work he carried out over the next decade led him to discover and then publish his first “big idea” [2]. This launched him on an academic career as a researcher in numerical analysis. Broyden himself attributed his unusual career trajectory (from a programmer in an engineering company to a chair in Computer Science at the University of Essex) to just having been at the right time at the right place [1]. In making this self-deprecating remark, he was certainly underplaying his own particular gifts. But it is also true that the second half of the twentieth century was a rather special time in the development of computational mathematics; and the UK was rather a special place. I myself was caught up in a wave of inventiveness and experimentation within a community of researchers which, I shall argue, was similar to the company of writers and poets I am happy to belong to nowadays.
In the 1950s many large companies first got their hands on computers and had to begin working out what to do with them. Clearly they offered the possibility to do complicated calculations with more speed (and fewer errors) than any human being could achieve. But there were few experts in how to program them (US spelling soon became standard!) or indeed in deciding what calculations one could most usefully program. In other words there was a wide field to explore but very little received wisdom was available. In this situation anyone with a lively imagination (and perhaps an indifferent BSc) might stumble on a novel problem-solving approach which was better than the status quo. (In fact the status quo wasn’t all that static. Computers in the 1950s and 1960s were getting faster all the time but scientists and engineers kept pushing them to their limits. Satisfaction at being able to solve a problem in (say) ten variables quickly turned to frustration when the same approach couldn’t deal with a problem in 100 variables.) One could make comparisons with the early days of flying when progress was often based on an attitude of “let’s try this and see what happens”. However there wasn’t as much risk to life and limb from running an ill-conceived computer program as there was from flying a badly designed aircraft!
An illustration of how the use of computers changed the practice of applied mathematics is provided by the recent film Hidden Figures about the African-American mathematician Katherine Johnson who worked on NASA space programmes. An essential element in planning a spacecraft mission is the ability to calculate the trajectory of a vehicle moving under gravity with or without thrust from on-board motors. Such trajectory calculations require the solution of a system of differential equations; and for a long time the scientists at NASA tried to find ingenious analytical solutions – essentially they were looking for algebraic formulae that would define the spacecraft’s path. This approach did not prove successful and the film portrays a “breakthrough moment” when Katherine Johnson suggests using Euler’s method. Essentially this involves using the differential equations to approximate the spacecraft’s motion over very many tiny time-steps – the smaller the steps the greater the accuracy. The resulting lengthy calculation is well-suited to a computer but is pretty demanding for a human being! Nevertheless it does provide a plausible way of estimating the trajectory followed by an actual spacecraft.
Once the basic notion of using the 250 year old Euler method to simulate real-world behaviour had been accepted then further possibilities opened up. People soon discovered all sorts of refinements of the technique which yielded better accuracy and/or required less computing effort. At the same time there was a similar search for improvements in many other tools of numerical mathematics, such as iterative methods for solving highly complicated equations via sequences of improving approximations (as outlined in an appendix). The speed of convergence to the right answer could be increased by more and more cunning use of information about one incorrect estimate in order to generate a better one.
So, from the 1950s onwards, there grew up a generation of programmers, designers, engineers and academics, whose work required them to be constantly improving currently available computing methods – or even inventing methods where none previously existed. In this sort of research, imagination, intuition, and sometimes analogy and pictorial thinking would often play as much of a part as rigorous analysis. The imaginative reader may be able to picture these individuals in offices, laboratories and also at home, busily developing and refining algorithms (or apps as we might now call them). They might have single specific problem in mind but often they would cherish the hope that their solution techniques would gain wider acceptance and use. And I, dear reader, was one of them, beginning in the aircraft industry and then switching to a technical college which reinvented itself during my career as a polytechnic and then as a university.
We merely need to interchange ‘algorithm’ and ‘poem’ to see similarities between the situation I have just described and the one that poets find themselves in. One way for a new algorithm to get attention would be via a seminar – which is pretty much what poets would call a reading. Just as one might go to hear work by a new or a well-known poet, so I used to spend pleasant afternoons visiting universities or research institutes, often in attractive locations (e.g. the National Physical Laboratory is alongside Bushey Park and the Rutherford Laboratories nestle in the Oxfordshire countryside). My purpose would be to critique (or perhaps appropriate} some new ideas relevant to what I was working on. And there would be tea and (sometimes) biscuits afterwards! Poets will not be surprised to learn that, during conversations over these refreshments, one would probably badger the organisers for an invitation to present one’s own new work in the near future. The underlying hope was that an appearance at one of these low-key afternoon seminars would lead to one being asked to speak at a big academic conference – roughly the equivalent of a poetry festival. (I will say, however, that it always seemed easier to get a spot at an academic conference than it does nowadays to get a reading at a festival!)
But beyond these oral presentations it was publication in print that was a higher goal. An algorithm might get real fame if it appeared in a sufficiently prestigious journal. People still refer to – and use – Broyden’s method over fifty years after it was published. (Another way of becoming an indexed name in the literature is to invent a problem which is very difficult to solve since all one’s contemporaries and successors will need to demonstrate that their method can indeed solve it!) There was of course a hierarchy of journals, just as there is in poetry; and one had to be honest and self-aware enough to know one’s place. Some journals would only consider algorithms accompanied by a rigorous mathematical analysis; others were content to publish a promising idea backed up only by experimental evidence (and some enthusiastic spin on the results!). Then again some journals would print in-depth case studies involving one specific problem while others were only interested in algorithms which could claim wide applicability. These distinctions are not unlike the differences between poetry publications deemed ‘academic’ or ‘formal’ and those which value ‘accessibility’ or ‘diversity’.
Interestingly, most of my mathematical acquaintances were content to accumulate magazine appearances and, unlike poets, did not fret about gathering them into a collection! But one final accolade that mathematicians and poets could both aspire to was The Big Prize. Awards for algorithmic innovation are far fewer than the array of poetry prizes offered every year from the small and local to the big and international. This comparison is somewhat misleading however since all the mathematics awards that I am aware of resemble the Eliot or Forward prizes – that is they are given for already published work. I know of no instances of a ”competition algorithm” written specifically for a contest. Maybe this explains why, in my experience, mathematical prizes have not generated the level of debate and controversy that poetry prizes do.
There was of course a sense of competitiveness in all this. Reputation and career ambition were both motivating factors alongside the thrill of the chase for the perfect answer to a hard question. But I like to think that pure curiosity was the main driving force; and I can honestly say that didn’t see much evidence of jealousy or bitter rivalry during my years in computational mathematics. Even though we were working as individuals or in small teams there was a fairly widespread sense of being part of a collective project. What’s more, the projects we were engaged on were often collaborative and hence multi-author publications were commonplace, as in many other academic areas. But quite apart from conscious cooperation, a good many algorithms and theorems are known by the names of two or more originators who hit upon the same idea independently and were not over-anxious about trying to establish who got there first. For instance, credit for the important Broyden-Fletcher-Goldfarb-Shanno formula was very amicably shared between four authors – as can be seen in the famous but fuzzy photograph at the head of this article, in which the presence of several beer mugs indicates a genuinely convivial atmosphere. (As a matter of fact I was present when that photograph was taken; and it now strikes me that poets would be more likely to be holding glasses of wine.) Of course academic authorship can be a different from literary authorship and plagiarism of a poem is not at all the same thing as two people stumbling on a similar answer to an existing question.
Interestingly, the grounds for disputing the advantages of rival mathematical techniques could melt away rather suddenly and disconcertingly. I recall a time in the 1970s when the merits of a number of competing iterative methods were being quite hotly argued – until that is one of my work colleagues, Laurence Dixon [3], proved that all the methods were theoretically equivalent! Any observed differences in behaviour between the methods were in fact due to tiny rounding errors in arithmetic which can sometimes get magnified during a long calculation and greatly distort the final result – a computational version of the apocryphal butterfly wing effect in meteorology [4]. Real numbers will never behave exactly as we would like them to and cumulative rounding errors can be hard to detect and require ingenuity to overcome. But as is observed in the haiku that Lennon & McCartney almost wrote (whose relevance Philip Gill, Walter Murray & Margaret Wright [5] may have been the first to notice)
You can get it wrong but still think that it’s all right. We can work it out.
I retired from the fray in 2008; but something of that optimistically playful spirit probably still continues in my old area of mathematical study even though the landscape of open questions that was relatively unexplored fifty years ago is now pretty well covered by roads, signposts and fences, the best of the last century’s enthusiastic speculations and experiments having been formalised into a body of received wisdom. In fact I haven’t quit the field entirely and still potter about as an amateur, since
The ground is well mapped but we keep on exploring: there might be short cuts!
Mathematicians can drop out of sight quite quickly when they retire: the stream of published papers dries up and they will seldom be seen at seminars or conferences. Poets on the other hand can rarely be said to have retired and, even if they are not writing as much as they once did, it is not unusual for them to attend readings and festivals and the possibility of one more slim volume may not be entirely ruled out…. Mathematicians however, like other academics, do have one advantage in terms of longer-lasting recognition: and that is the citation. If a poet’s books go out of print then at least some individual poems may survive in major anthologies. But this will be a consolation offered to relatively few of us. Papers by mathematicians can have quite a long post-publication life because current researchers are expected to cite pioneering work in their area of study. I am still registered with an archiving website (like one’s Facebook page these things never die of their own accord) which informs me every week that sundry papers of mine – some from as long ago as 1971 – have been included in various reference lists. This may mean that the paper referred to has actually been read by some fresh-faced youngster; but that fond hope cannot be taken for granted! I know this because one of my most-cited articles doesn’t actually exist! The actual title of one of my papers was misquoted in a long-ago citation by a careless author and then sent for printing by a careless proof-reader – and those spurious publication details have now been cut-and-pasted across the literature. Which, now I come to think of it, is rather like the spread of rounding-error throughout a calculation. The poetic equivalent, I suppose, would be for a typo to appear in a poem-extract quoted in a major review – or worse still in a prestigious anthology! Perhaps it boils down to
Well-earned neglect or immortality (of sorts) on false pretences?
References [1] Andreas, Griewank (2011). “Obituary for Charles Broyden”. Optimization Methods and Software. 26 (3): 343–344 [2] Broyden, C. G. (October 1965). “A Class of Methods for Solving Nonlinear Simultaneous equations”. Mathematics of Computation. American Mathematical Society.19 (2): 577–593 [3] Dixon L C W (February 1972) “Quasi-Newton algorithms generate identical points” Mathematical Programming2(1):383-387 [4] https://en.wikipedia.org/wiki/Butterfly_effect [5] Gill PE & Murray W, Practical Optimization, Academic Press 1982
Appendix For the benefit of the bolder or more curious reader we can illustrate the idea of iteration by showing bow to solve a problem by a sequence of improving approximations. Suppose we want to work out the square root of a number n. If x0 denotes some arbitrarily guessed value for the square root of n it can be proved that a better estimate is given by
x1 = (x02 + n)/(2x0)
A better estimate still is then obtained by using the formula again
x2 = (x12 + n)/(2x1)
and yet again
x3 = (x22 + n)/(2x2)
We can keep on using this formula until the sequence of estimates converges – i.e. successive estimates are effectively the same. This value is the square root we are seeking. The reader can verify that if n is 4 and we use the initial guess x0 =3 the subsequent estimates would be
x1 = 2.1667, x2 = 2.0064, x3 = 2.0000
So the iterations are converging very rapidly. This technique is known as Newton’s method and is even older than Euler’s method! It will work for finding the square root of any number and success does not depend on making a good initial guess x0. Readers may like to try finding other square roots – but be warned: playing with iteration can be addictive!
Dec 11 2019
When Pythagoras met Homer
When Pythagoras met Homer: Michael Bartholomew-Biggs recalls a time when being a mathematician was like being a poet.
I suspect few London Grip readers will have heard of Charles Broyden (1933-2011) even though he is the originator of one of the twentieth century’s most significant ideas in computational mathematics. Non-mathematical readers may be relieved to learn that I won’t be trying to explain what this idea was (although a few key expressions appear in the image on the right)!
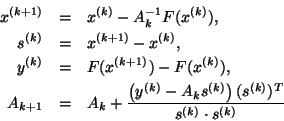
This article – which I hope will be of interest to non mathematicians – has its origins in a quotation from Broyden’s obituary [1] which states – using the subject’s own words – that he left university in 1955 armed with an indifferent bachelor’s degree in physics and an uncertain hold on linear algebra. These qualifications were enough to secure him a job in industry and the work he carried out over the next decade led him to discover and then publish his first “big idea” [2]. This launched him on an academic career as a researcher in numerical analysis. Broyden himself attributed his unusual career trajectory (from a programmer in an engineering company to a chair in Computer Science at the University of Essex) to just having been at the right time at the right place [1]. In making this self-deprecating remark, he was certainly underplaying his own particular gifts. But it is also true that the second half of the twentieth century was a rather special time in the development of computational mathematics; and the UK was rather a special place. I myself was caught up in a wave of inventiveness and experimentation within a community of researchers which, I shall argue, was similar to the company of writers and poets I am happy to belong to nowadays.
In the 1950s many large companies first got their hands on computers and had to begin working out what to do with them. Clearly they offered the possibility to do complicated calculations with more speed (and fewer errors) than any human being could achieve. But there were few experts in how to program them (US spelling soon became standard!) or indeed in deciding what calculations one could most usefully program. In other words there was a wide field to explore but very little received wisdom was available. In this situation anyone with a lively imagination (and perhaps an indifferent BSc) might stumble on a novel problem-solving approach which was better than the status quo. (In fact the status quo wasn’t all that static. Computers in the 1950s and 1960s were getting faster all the time but scientists and engineers kept pushing them to their limits. Satisfaction at being able to solve a problem in (say) ten variables quickly turned to frustration when the same approach couldn’t deal with a problem in 100 variables.) One could make comparisons with the early days of flying when progress was often based on an attitude of “let’s try this and see what happens”. However there wasn’t as much risk to life and limb from running an ill-conceived computer program as there was from flying a badly designed aircraft!
So, from the 1950s onwards, there grew up a generation of programmers, designers, engineers and academics, whose work required them to be constantly improving currently available computing methods – or even inventing methods where none previously existed. In this sort of research, imagination, intuition, and sometimes analogy and pictorial thinking would often play as much of a part as rigorous analysis. The imaginative reader may be able to picture these individuals in offices, laboratories and also at home, busily developing and refining algorithms (or apps as we might now call them). They might have single specific problem in mind but often they would cherish the hope that their solution techniques would gain wider acceptance and use. And I, dear reader, was one of them, beginning in the aircraft industry and then switching to a technical college which reinvented itself during my career as a polytechnic and then as a university.
But beyond these oral presentations it was publication in print that was a higher goal. An algorithm might get real fame if it appeared in a sufficiently prestigious journal. People still refer to – and use – Broyden’s method over fifty years after it was published. (Another way of becoming an indexed name in the literature is to invent a problem which is very difficult to solve since all one’s contemporaries and successors will need to demonstrate that their
method can indeed solve it!) There was of course a hierarchy of journals, just as there is in poetry; and one had to be honest and self-aware enough to know one’s place. Some journals would only consider algorithms accompanied by a rigorous mathematical analysis; others were content to publish a promising idea backed up only by experimental evidence (and some enthusiastic spin on the results!). Then again some journals would print in-depth case studies involving one specific problem while others were only interested in algorithms which could claim wide applicability. These distinctions are not unlike the differences between poetry publications deemed ‘academic’ or ‘formal’ and those which value ‘accessibility’ or ‘diversity’.
Interestingly, most of my mathematical acquaintances were content to accumulate magazine appearances and, unlike poets, did not fret about gathering them into a collection! But one final accolade that mathematicians and poets could both aspire to was The Big Prize. Awards for algorithmic innovation are far fewer than the array of poetry prizes offered every year from the small and local to the big and international. This comparison is somewhat misleading however since all the mathematics awards that I am aware of resemble the Eliot or Forward prizes – that is they are given for already published work. I know of no instances of a ”competition algorithm” written specifically for a contest. Maybe this explains why, in my experience, mathematical prizes have not generated the level of debate and controversy that poetry prizes do.
There was of course a sense of competitiveness in all this. Reputation and career ambition were both motivating factors alongside the thrill of the chase for the perfect answer to a hard question. But I like to think that pure curiosity was the main driving force; and I can honestly say that didn’t see much evidence of jealousy or bitter rivalry during my years in computational mathematics. Even though we were working as individuals or in small teams there was a fairly widespread sense of being part of a collective project. What’s more, the projects we were engaged on were often collaborative and hence multi-author publications were commonplace, as in many other academic areas. But quite apart from conscious cooperation, a good many algorithms and theorems are known by the names of two or more originators who hit upon the same idea independently and were not over-anxious about
trying to establish who got there first. For instance, credit for the important Broyden-Fletcher-Goldfarb-Shanno formula was very amicably shared between four authors – as can be seen in the famous but fuzzy photograph at the head of this article, in which the presence of several beer mugs indicates a genuinely convivial atmosphere. (As a matter of fact I was present when that photograph was taken; and it now strikes me that poets would be more likely to be holding glasses of wine.) Of course academic authorship can be a different from literary authorship and plagiarism of a poem is not at all the same thing as two people stumbling on a similar answer to an existing question.
You can get it wrong
but still think that it’s all right.
We can work it out.
I retired from the fray in 2008; but something of that optimistically playful spirit probably still continues in my
old area of mathematical study even though the landscape of open questions that was relatively unexplored fifty years ago is now pretty well covered by roads, signposts and fences, the best of the last century’s enthusiastic speculations and experiments having been formalised into a body of received wisdom. In fact I haven’t quit the field entirely and still potter about as an amateur, since
The ground is well mapped
but we keep on exploring:
there might be short cuts!
Mathematicians can drop out of sight quite quickly when they retire: the stream of published papers dries up and they will seldom be seen at seminars or conferences. Poets on the other hand can rarely be said to have retired and, even if they are not writing as much as they once did, it is not unusual for them to attend readings and festivals and the possibility of one more slim volume may not be entirely ruled out…. Mathematicians however, like other academics, do have one advantage in terms of longer-lasting recognition: and that is the citation. If a poet’s books go out of print then at least some individual poems may survive in major anthologies. But this will
be a consolation offered to relatively few of us. Papers by mathematicians can have quite a long post-publication life because current researchers are expected to cite pioneering work in their area of study. I am still registered with an archiving website (like one’s Facebook page these things never die of their own accord) which informs me every week that sundry papers of mine – some from as long ago as 1971 – have been included in various reference lists. This may mean that the paper referred to has actually been read by some fresh-faced youngster; but that fond hope cannot be taken for granted! I know this because one of my most-cited articles doesn’t actually exist! The actual title of one of my papers was misquoted in a long-ago citation by a careless author and then sent for printing by a careless proof-reader – and those spurious publication details have now been cut-and-pasted across the literature. Which, now I come to think of it, is rather like the spread of rounding-error throughout a calculation. The poetic equivalent, I suppose, would be for a typo to appear in a poem-extract quoted in a major review – or worse still in a prestigious anthology! Perhaps it boils down to
Well-earned neglect or
immortality (of sorts)
on false pretences?
References
[1] Andreas, Griewank (2011). “Obituary for Charles Broyden”. Optimization Methods and Software. 26 (3): 343–344
[2] Broyden, C. G. (October 1965). “A Class of Methods for Solving Nonlinear Simultaneous equations”. Mathematics of Computation. American Mathematical Society.19 (2): 577–593
[3] Dixon L C W (February 1972) “Quasi-Newton algorithms generate identical points” Mathematical Programming 2(1):383-387
[4] https://en.wikipedia.org/wiki/Butterfly_effect
[5] Gill PE & Murray W, Practical Optimization, Academic Press 1982
Appendix
For the benefit of the bolder or more curious reader we can illustrate the idea of iteration by showing bow to solve a problem by a sequence of improving approximations. Suppose we want to work out the square root of a number n. If x0 denotes some arbitrarily guessed value for the square root of n it can be proved that a better estimate is given by
x1 = (x02 + n)/(2x0)
A better estimate still is then obtained by using the formula again
x2 = (x12 + n)/(2x1)
and yet again
x3 = (x22 + n)/(2x2)
We can keep on using this formula until the sequence of estimates converges – i.e. successive estimates are effectively the same. This value is the square root we are seeking. The reader can verify that if n is 4 and we use the initial guess x0 =3 the subsequent estimates would be
So the iterations are converging very rapidly. This technique is known as Newton’s method and is even older than Euler’s method! It will work for finding the square root of any number and success does not depend on making a good initial guess x0. Readers may like to try finding other square roots – but be warned: playing with iteration can be addictive!